The Strong form of mathematical induction
The strong form of mathematical induction is so called because the hypotheses one uses are stronger. It comes in various names, strong induction is also called the principle of complete induction (PCI), also known as the course-of-values induction.
Instead of showing that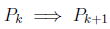 
in the inductive step, we get to assume that all statements numbered smaller than 
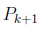are true.
The statement that needs to be proved is,
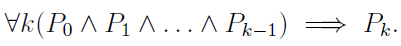
This outline will help you have the complete picture of PCI.
Disclaimer: this is a summary of section 5.4 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.
It should also be noted that 'strong' and 'weak' induction are logically equivalent. You can prove one from the other and vice versa.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
That's right they are logically equivalent. The difference lies in the process, which needs to be emphasize.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I want to learn math. but math hates me :( hahah i dont really understand . peace
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Great post!
Thanks for tasting the eden!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You got a 7.16% upvote from @minnowvotes courtesy of @sinbad989!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Wow greate article!
Thanks for using the @postdoctor service!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit